Determination of g using a vertical mass-spring system

Experiment to determine acceleration due to gravity (g) using a vertical mass-spring system by measuring displacement and vibration time periods.

APPARATUS:

Soft slinky helical spring, pointer with two holes, slotted weight set, tall iron stand fitted with cm. scale and spring suspending support, stop watch.

PROCEDURE:

1. Suspended the spring vertically from the support at the top of the iron stand. Attach the plastic pointer to the lower end of the spring from the upper hole. Attach the slotted weight hanger from the lower hole, as shown in the diagram.
2. Adjust the height of the spring support and the position of the cm. scale on the iron stand such that the plastic pointer approximately coincides with zero of the cm. scale. Note the position of the pointer.
3. Put one slotted weight in the hanger. Carefully note the position on the scale and record the displacement (x) of the spring in your table of observations.
4.  Slightly pull the weight down and then release it. The weight vibrates vertically. Note the time for 20 vibrations twice. Record these times in your table. Also, calculate the time period of vibrations (T). Calculate the ratio x/T².
5.  Remove the slotted weight from the hanger. Check the position of the pointer and note it.
6.  Now add two slotted weights to the hanger. Again, record the displacement produced in the spring. Repeat step 4.
7.  Take several readings of displacement and the corresponding time periods, increasing slotted weights each time. Calculate the mean value of x/T². Use this value in the relation.

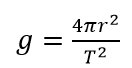
OBSERVATIONS:

No of Obs.	Initial position of the pointer X1 (cm)	Weight added to the hanger (g)	Position of the pointer with weight X2 (cm)	Displace -ment X=x2 –x1 (cm)	t1=(s)	t2= (s)		T=t/20	(cm/s2)
1. 2. 3. 4. 5.	0.3 0.3 0.4 0.4 0.5	50 100 150 200 250	9.4 18.3 27.5 36.3 45.3	9.1 18.0 27.1 35.9 44.8	12.22 17.19 20.82 24.05 26.80	12.32 17.03 20.82 24.03 26.86	12.27 17.03 20.82 24.03 26.86	0.67 0.85 1.04 1.20 1.34	24.46 24.91 25.06 24.93 24.95

PRECAUTIONS

1. The apparatus must be vertical.
2. Displacement must be noted carefully.

                                              VIVA VOCE

Q.1.           What will happen to the time period of a vertical mass spring system if it is taken from Earth to the Moon?

Ans.          It will remain the same. But the values of displacement and acceleration of free fall will change.

Q.2.           Will this method give the same value of acceleration of free fall in winter and summer?

Ans.          No, because the spring constant of the spring changes with temperature.

Q.3.           What is Hook’s law?

Ans.          It states that within elastic limits, stress is proportional to strain.

Q.4.           What is Young’s Modulus?

Ans.          It is the ratio of stress to longitudinal strain.

Q.5.           Define P.E.

Ans.          The energy possessed by a body due to its position in the constraint field is called P.E.

Q.6.           How does the P.E. change to the mechanical P.E?

Ans.          It is due to the extension produced in the spring by placing a weight in the pan and then by determining its constant ‘K’.

Q.7.           Differentiate between F =–Kx in the case of mass mass-spring system            .

Ans.            F              = –K x represents the restoring force

                   F   = K x     represents the applied force in Hook’s law

Q.8.           What type of graph is obtained between tension and extension in the case of a helical spring?

Ans.          It will be a straight line graph, and its slope represents the force constant of the spring.

Q.9.           What type of energies are interchanged in the case of a mass suspended by a helical spring?

Ans.          Gravitational P.E. and Mechanical P.E.

Q.10.         Define elastic limit.

Ans.          The limit beyond which the body does not obey Hook’s law.

Q.11.         What is the value of ‘g at the center of the Earth?

Ans.          g=0, at the centre of the earth.

Q.12.         What is the dimension of the spring constant?

Ans.          [MT²]

Q.13.         Write down the characteristics of a simple harmonic motion.

Ans.          I – Acceleration is directly proportional to the displacement from the mean position.

                II – Acceleration is directed towards the mean position.

Q.14.         Define spring constant.

Ans.          It is equal to the force that causes unit extension in the spring.

Q.15.         What do you mean by Hook’s law?

Ans.          Within the elastic limit, extension produced in the spring is directly proportional to the applied force.